Januari 2024 - Belajar Matematika
Home
KELAS X
Materi BAB 1
Materi BAB 2
Materi BAB 3
Materi BAB 4
Materi BAB 5
Materi BAB 6
Materi BAB 7
Materi BAB 8
Materi BAB 9
KELAS XI
Materi BAB 1
Materi BAB 2
Materi BAB 3
Materi BAB 4
Materi BAB 5
Materi BAB 6
Materi BAB 7
Materi BAB 8
Materi BAB 9
KELAS XII
DropDown 1
DropDown 2
DropDown 3
Select Here
HOME
KELAS X
- MATERI BAB 1
- MATERI BAB 2
- MATERI BAB 3
- MATERI BAB 4
- MATERI BAB 5
- MATERI BAB 6
- MATERI BAB 7
- MATERI BAB 8
- MATERI BAB 9
KELAS XI
- MATERI BAB 1
- MATERI BAB 2
- MATERI BAB 3
- MATERI BAB 4
- MATERI BAB 5
- MATERI BAB 6
- MATERI BAB 7
- MATERI BAB 8
- MATERI BAB 9
KELAS XII
- DROPDOWN 1
- DROPDOWN 2
- DROPDOWN 3
skip to main
|
skip to sidebar
Read More
regresi linear dan contohnya
Read More
regresi linear
Read More
Ruang Pintar Kumer xi2
Read More
E-Book
Read More
Diagram pencar dengan TIK
Read More
cara buat diagram Pencar
Read More
Data Bivariat Statistika
Read More
Lingkaran
Read More
posisi garis terhadap lingkaran
Read More
Relasi dan Fungsi
Read More
Program linear
Read More
Invers Fungsi Komposisi
Read More
Pengertian Diagram Pencar
Read More
bab 3
« Prev Movie
Next Movie »
Beranda
Alat Evaluasi
Sumatif 1
Sumatif 2
sumatif 3
PAS
Popular Posts
Pengertian Diagram Pencar
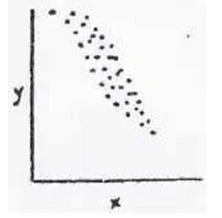
Diagram Pencar 1.1 Pengertian Diagram Pencar Diagram pencar adalah diagram yang paling sederhana dan efektif untu...
Statistika - Diagram Pencar
Simbol & Notasi
Diberdayakan oleh
Blogger
.
Submit Video
Blog Archive
▼
2024
(27)
►
Agustus
(2)
►
April
(1)
►
Februari
(3)
▼
Januari
(21)
regresi linear dan contohnya
regresi linear
Ruang Pintar Kumer xi2
E-Book
Diagram pencar dengan TIK
cara buat diagram Pencar
Data Bivariat Statistika
Lingkaran
posisi garis terhadap lingkaran
Relasi dan Fungsi
Program linear
Invers Fungsi Komposisi
Pengertian Diagram Pencar
bab 3
Statistika - Diagram Pencar
PAS 2023
E-BOOK
fungsi eks dan log
Jenis Bilangan
video Komposisi Fungsi
Video Belajar
►
2021
(2)
►
Desember
(2)
Cari Blog Ini
Arsip Blog
Agustus 2024
(2)
April 2024
(1)
Februari 2024
(3)
Januari 2024
(21)
Desember 2021
(2)
Laporkan Penyalahgunaan
Beranda
Mengenai Saya
Mat pm
Lihat profil lengkapku
Created By
SoraTemplates
| Distributed By
Gooyaabi Themes
